LintCode部分二叉树问题题解

纠错 31 Jan 2016

LintCode 66: Binary Tree Preorder Traversal (二叉树的前序遍历)

题目链接: http://www.lintcode.com/zh-cn/problem/binary-tree-preorder-traversal/

递归写法：

class Solution {
public:
    /**
     * @param root: The root of binary tree.
     * @return: Preorder in vector which contains node values.
     */
    vector<int> preorderTraversal(TreeNode *root) {
        // recursion version, traverse
        vector<int> rst;
        helper(root, rst);
        return rst;
    }
private:
    void helper(TreeNode *root, vector<int>& rst)
    {
        if (root == NULL) {
            return;
        }
        rst.push_back(root->val);
        helper(root->left, rst);
        helper(root->right, rst);
    }
};

非递归写法：

class Solution {
public:
    /**
     * @param root: The root of binary tree.
     * @return: Preorder in vector which contains node values.
     */
    vector<int> preorderTraversal(TreeNode *root) {
        // non-recursion version 1
        vector<int> rst;
        stack<TreeNode*> stacknode;
        TreeNode *curt = root;

        if (root == NULL) {
            return rst;
        }

        while (curt != NULL || !stacknode.empty()) {
            while (curt != NULL) {
                rst.push_back(curt->val);
                stacknode.push(curt);
                curt = curt->left;
            }
            curt = stacknode.top();
            stacknode.pop();
            curt = curt->right;
        }

        return rst;
    }
};

LintCode 67: Binary Tree Inorder Traversal (二叉树的中序遍历)

题目链接: http://www.lintcode.com/zh-cn/problem/binary-tree-inorder-traversal/

递归写法：

class Solution {
    /**
     * @param root: The root of binary tree.
     * @return: Inorder in vector which contains node values.
     */
public:
    vector<int> inorderTraversal(TreeNode *root) {
        // recursion version
        vector<int> inorder_node;
        if (root == NULL) {
            return inorder_node;
        }
        helper(root, inorder_node);
        return inorder_node;
    }

    void helper(TreeNode *root, vector<int>& inorder_node)
    {
        if (root == NULL) {
            return;
        }
        helper(root->left, inorder_node);
        inorder_node.push_back(root->val);
        helper(root->right, inorder_node);
    }
};

非递归写法：

class Solution {
public:
    vector<int> inorderTraversal(TreeNode *root) {
        // non-recursion version
        stack<TreeNode*> mystack;
        vector<int> rst;
        TreeNode *curt = root;
        while (curt != NULL || !mystack.empty()) {
            while (curt != NULL) {
                mystack.push(curt);
                curt = curt->left;
            }
            curt = mystack.top();
            rst.push_back(curt->val);
            mystack.pop();
            curt = curt->right;
        }
        return rst;
    }
};

LintCode 68: Binary Tree Postorder Traversal (二叉树的后序遍历)

链接: http://www.lintcode.com/zh-cn/problem/binary-tree-postorder-traversal/

递归写法：

class Solution {
    /**
     * @param root: The root of binary tree.
     * @return: Postorder in vector which contains node values.
     */
public:
    vector<int> postorderTraversal(TreeNode *root) {
        // recursion version
        vector<int> rst;
        postorder(root, rst);
        return rst;
    }
private:
    void postorder(TreeNode *root, vector<int>& rst)
    {
        if (root == NULL) {
            return;
        }
        postorder(root->left, rst);
        postorder(root->right, rst);
        rst.push_back(root->val);
    }
};

相比前两种遍历方法的非递归版本，非递归的后序遍历是最困难的。因为要访问完左子树和右子树之后才能访问根节点，而要想访问左子树和右子树，就必须先到达根节点才行，这意味着，在用栈实现时，一个节点将两次出现在栈顶，只有第二次出现在栈顶时，才能出栈并访问。

思路：用一个变量lastVisited标记上一次访问的节点，据此可判断一个节点的右子树是否已经被访问过。

先将根节点入栈，然后一直沿左子树进行DFS，中途将所有节点入栈，直到叶子节点；
此时不能立即弹出栈顶元素并输出其值，因为其右孩子还没有被访问；
如果栈顶元素的右孩子不为空，则按步骤1的方法处理右子树；否则可以弹出栈顶元素并输出其值，注意更新lastVisited变量（指向被弹出的栈顶节点）

class Solution {
    /**
     * @param root: The root of binary tree.
     * @return: Postorder in vector which contains node values.
     */
public:
    vector<int> postorderTraversal(TreeNode *root) {
        // non-recursion
        vector<int> rst;
        stack<TreeNode *> stacknode;

        TreeNode *curt = root, *lastVisited = NULL;

        while (curt != NULL || !stacknode.empty()) {
            while (curt != NULL) {
                stacknode.push(curt);
                curt = curt->left;
            }
            curt = stacknode.top();
            if (curt->right == NULL || lastVisited == curt->right) {
                stacknode.pop();
                rst.push_back(curt->val);
                lastVisited = curt;
                curt = NULL;    // 这句很关键，不能漏
            } else {
                curt = curt->right;
            }
        }
        
        return rst;
    }
};

LintCode 97: Max Depth of Binary Tree (二叉树的最大深度)

思路: 若根节点为空，最大深度为0；否则最大深度为1 + max(左子树的最大深度, 右子树的最大深度)。递归做就好。

class Solution {
public:
    /**
     * @param root: The root of binary tree.
     * @return: An integer
     */
    int maxDepth(TreeNode *root) {
        if (root == NULL) {
            return 0;
        }
        return max(maxDepth(root->left), maxDepth(root->right)) + 1;
    }
};

LintCode 93: Balanced Binary Tree (平衡二叉树)

思路1：直接根据定义：左、右子树都是平衡二叉树，并且左子树和右子树的高度之差不会超过1。

class Solution {
public:
    /**
     * @param root: The root of binary tree.
     * @return: True if this Binary tree is Balanced, or false.
     */
    bool isBalanced(TreeNode *root) {
        if (root == NULL) {
            return true;
        }
        if (isBalanced(root->left) && isBalanced(root->right) && 
            abs(maxDepth(root->left)-maxDepth(root->right)) <= 1) {
            return true;
        }
    }

private:
    int maxDepth(TreeNode *root)
    {
        if (root == NULL) {
            return 0;
        }
        return 1 + max(maxDepth(root->left), maxDepth(root->right));
    }
};

用了一个辅助函数maxDepth()来计算子树的最大深度。对当前根节点，调用maxDepth()计算左、右子树的高度将访问每一个节点，O(N)，由于对每一个节点都调用一次maxDepth()，所以总的时间复杂度是O(N^2)。

思路2：其实不必精确计算每个节点的高度，因为我们的目标只是判断一颗二叉树是否平衡。我们将高度信息利用起来，如果子树不平衡，就将它的高度置为-1，这样就能根据高度立即知道以某节点为根的树是否是平衡的了，而不用再去计算另一颗子树的高度。

class ResultType {
public:
    bool isBalanced;
    int maxDepth;
    ResultType(bool isBalanced, int maxDepth) {
        this->isBalanced = isBalanced;
        this->maxDepth = maxDepth;
    }
};

class Solution {
public:
    /**
     * @param root: The root of binary tree.
     * @return: True if this Binary tree is Balanced, or false.
     */
    bool isBalanced(TreeNode *root) {
        return helper(root).isBalanced;
    }

private:
    ResultType helper(TreeNode *root)
    {
        if (root == NULL) {
            return ResultType(true, 0);
        }

        ResultType left = helper(root->left);
        ResultType right = helper(root->right);
        // subtree not balanced
        if (!left.isBalanced || !right.isBalanced) {
            return ResultType(false, -1);
        }
        // root not balanced
        if (abs(left.maxDepth - right.maxDepth) > 1) {
            return ResultType(false, -1);
        }

        return ResultType(true, max(left.maxDepth, right.maxDepth) + 1);
    }
};

上面的代码参考了<a href=”http://www.jiuzhang.com/solutions/balanced-binary-tree/”, target=”_blank”>这里</a>，定义了一个ResultType类，来保存“子树是否平衡”和“子树的最大深度”两个信息，这样可以有效减少递归调用的次数。

另一种简洁的实现方法：

class Solution {
public:
    bool isBalanced(TreeNode *root) {
        return dfsHeight (root) != -1;
    }
private:
    int dfsHeight (TreeNode *root) {
        if (root == NULL) return 0;

        int leftHeight = dfsHeight (root -> left);
        if (leftHeight == -1) return -1;
        int rightHeight = dfsHeight (root -> right);
        if (rightHeight == -1) return -1;

        if (abs(leftHeight - rightHeight) > 1)  return -1;

        return max (leftHeight, rightHeight) + 1;
    }
};

LintCode 88: Lowest Common Ancestor (最近公共祖先)

思路：

如果A或B就是根节点，则根节点可能是A, B的LCA，返回根节点，否则转2；
分治： 2.1 Divide: 分别在左子树和右子树计算LCA(A, B)； 2.2 Conquer: 如果左子树计算的结果和右子树计算的结果都不为空，则根节点就是A, B的LCA；如果左不为空而右为空，则返回左子树的计算结果；否则返回右子树的计算结果。

class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        if (root == NULL) {
            return NULL;
        }
        if (p == root || q == root) {
            return root;
        }
        TreeNode *left = lowestCommonAncestor(root->left, p, q);
        TreeNode *right = lowestCommonAncestor(root->right, p, q);
        if (left != NULL && right != NULL) {
            return root;
        }
        if (left != NULL) {
            return left;
        }
        if (right != NULL) {
            return right;
        }
        return NULL;
    }
};

LintCode 94: Binary Tree Maximum Path Sum (二叉树中的最大路径和)

很好的题目，也有难度。但是理清楚了，就不难啦~

思路：

最优路径上的节点一定是连续的，不能中断
最优路径中一定包含某个子树的根节点
写一个递归函数，实现计算从某个根节点出发能够达到的单条最大路径和；同时计算穿过根节点的最大路径和，用一个全局变量保存最优解。

class Solution {
public:
    int rst;
    /**
     * @param root: The root of binary tree.
     * @return: An integer
     */
    int maxPathSum(TreeNode *root) {
        rst = 0x80000000;
        helper(root);
        return rst;
    }

private:
    int helper(TreeNode *root) {
        if (root == NULL) {
            return 0;
        }
        // divide
        int left = helper(root->left);
        left = max(0, left);
        int right = helper(root->right);
        right = max(0, right);
        // conquer
        int single_path = max(left, right) + root->val;
        int double_path = left + right + root->val;
        rst = max(rst, max(single_path, double_path));
        return single_path;
    }
};

LintCode 69: Binary Tree Level Order Traversal (二叉树的层次遍历)

思路：

用一个队列存放二叉树每一层的节点
用一个变量levelnum保存二叉树每一层的节点数
在一次遍历队列中（遍历的节点数为levelnum），每访问一个节点，就将该节点的两个后继节点入队（如果有的话），然后将该节点出队
直到队列为空

class Solution {
public:
    vector<vector<int> > levelOrder(TreeNode* root) {
        vector<vector<int> > rst;
        if (root == NULL) {
            return rst;
        }
        queue<TreeNode*> myqueue;
        myqueue.push(root);
        int level = 0, levelnum = myqueue.size();
        TreeNode *current;
        while (!myqueue.empty()) {
            vector<int> tmp;
            for (int i = 1; i <= levelnum; ++i) {
                current = myqueue.front();
                tmp.push_back(current->val);
                if (current->left != NULL) {
                    myqueue.push(current->left);
                }
                if (current->right != NULL) {
                    myqueue.push(current->right);
                }
                myqueue.pop();
            }
            rst.push_back(tmp);
            level++;
            levelnum = myqueue.size();
        }
        return rst;
    }
};

LintCode 70: Binary Tree Level Order Traversal II

思路：在上一题(LintCode 69)的结果上reverse一下即可(函数头文件: algorithm，当然也可以自己写)。

class Solution {
    /**
     * @param root : The root of binary tree.
     * @return : buttom-up level order a list of lists of integer
     */
public:
    vector<vector<int> > levelOrderBottom(TreeNode *root) {
        vector<vector<int> > rst;
        if (root == NULL) {
            return rst;
        }
        queue<TreeNode*> myqueue;
        myqueue.push(root);
        int curLevelNum = 1;
        TreeNode *current;
        while (!myqueue.empty()) {
            vector<int> curLevelRst;
            for (int i = 1; i <= curLevelNum; ++i) {
                current = myqueue.front();
                curLevelRst.push_back(current->val);
                myqueue.pop();
                if (current->left != NULL) {
                    myqueue.push(current->left);
                }
                if (current->right != NULL) {
                    myqueue.push(current->right);
                }
            }
            rst.push_back(curLevelRst);
            curLevelNum = myqueue.size();
        }
        reverse(rst.begin(), rst.end());    // 就增加了这行
        return rst;
    }
};

LintCode 71: Binary Tree Zigzag Level Order Travsersal (二叉树锯齿形层次遍历)

思路1：二叉树层次遍历的变形，多加一个判断就好，如果是从右到左，就把该层结果reverse一下。

class Solution {
    /**
     * @param root: The root of binary tree.
     * @return: A list of lists of integer include 
     *          the zigzag level order traversal of its nodes' values 
     */
public:
    vector<vector<int> > zigzagLevelOrder(TreeNode *root) {
        vector<vector<int> > rst;
        if (root == NULL) {
            return rst;
        }
        queue<TreeNode*> myqueue;
        myqueue.push(root);
        int curLevelNum = 1;
        TreeNode *current;
        bool fromLToR = false;
        while (!myqueue.empty()) {
            vector<int> curLevelRst;
            for (int i = 1; i <= curLevelNum; ++i) {
                current = myqueue.front();
                curLevelRst.push_back(current->val);
                myqueue.pop();
                if (current->left != NULL) {
                    myqueue.push(current->left);
                }
                if (current->right != NULL) {
                    myqueue.push(current->right);
                }
            }
            fromLToR = !fromLToR;
            if (fromLToR) {
                rst.push_back(curLevelRst);
            } else {
                reverse(curLevelRst.begin(), curLevelRst.end());
                rst.push_back(curLevelRst);
            }
            curLevelNum = myqueue.size();
        }
        
        return rst;        
    }
};

思路2: 用双端队列。

定义一个bool类型变量flag，初始化为true; 定义一个双端队列(deque):myqueue，用来存树上的节点; 定义一个vector: next_level，用来存每一层输出节点的值；
flag == true时，从队列的back取值，每考察一个节点，就把它的值加入next_level，并按先左后右的顺序在队列的front插入其儿子节点（如果有的话），然后将这个节点pop_back出队列；
flag == false时，从队列的front取值，每考察一个节点，就把它的值加入next_level，并按先右后左的顺序在队列的back插入其儿子节点（如果有），然后将这个节点pop_front出队列；
处理完一层后，记得更新flag: flag = !flag，并且清空next_level，以便下一次使用。

class Solution {
public:
    vector<vector<int>> zigzagLevelOrder(TreeNode *root) {
        // 2015-09-14, BY Mio
        vector<vector<int> > rst;
        vector<int> next_level;
        deque<TreeNode*> myqueue;
        int cnt;
        bool flag = true;

        if (root == NULL) {
            return rst;
        }
        myqueue.push_back(root);
        while (!myqueue.empty()) {
            cnt = myqueue.size();
            for (int i = 0; i < cnt; ++i) {
                if (flag == true) {
                    next_level.push_back(myqueue.back()->val);
                    if (myqueue.back()->left != NULL) {
                        myqueue.push_front(myqueue.back()->left);
                    }
                    if (myqueue.back()->right != NULL) {
                        myqueue.push_front(myqueue.back()->right);
                    }
                    myqueue.pop_back();
                } else {
                    next_level.push_back(myqueue.front()->val);
                    if (myqueue.front()->right != NULL) {
                        myqueue.push_back(myqueue.front()->right);
                    }
                    if (myqueue.front()->left != NULL) {
                        myqueue.push_back(myqueue.front()->left);
                    }
                    myqueue.pop_front();
                }
            }
            rst.push_back(next_level);
            flag = !flag;
            next_level.clear();
        }

        return rst;
    }
};

LintCode 95: Validate Binary Search Tree (验证二叉查找树)

思路：按BST的定义来就好。

如果左子树不是BST，则返回false；否则DFS计算左子树的最大值，如果其大于root->val，返回false；转2；
如果右子树不是BST，则返回false；否则DFS计算右子树的最小值，如果其小于root->val，返回false；转3；
1和2都顺利通过的话，到这步就返回true啦

class Solution {
public:
    /**
     * @param root: The root of binary tree.
     * @return: True if the binary tree is BST, or false
     */
    bool isValidBST(TreeNode *root) {
        if (root == NULL) {
            return true;
        }
        bool left = isValidBST(root->left);
        if (!left) {
            return false;
        }
        if (root->left != NULL) {
            int maxLeft = dfsMax(root->left);
            if (maxLeft >= root->val) {
                return false;
            }
        }
        bool right = isValidBST(root->right);
        if (!right) {
            return false;
        }
        if (root->right != NULL) {
            int minRight = dfsMin(root->right);
            if (minRight <= root->val) {
                return false;
            }
        }
        return true;
    }

private:
    int dfsMax(TreeNode *root) {
        while (root->right != NULL) {
            root = root->right;
        }
        return root->val;
    }

    int dfsMin(TreeNode *root) {
        while (root->left != NULL) {
            root = root->left;
        }
        return root->val;
    }
};

另外，关于这道题，这里给出了多种解法供参考。

LintCode 448: Inorder Successor in Binary Search Tree

http://www.lintcode.com/problem/validate-binary-search-tree/

思路

用DFS找p， O(h)。DFS的同时用一个变量lastVisited记录可能的inorder successor，初始化为NULL，更新这个变量的规则是：如果往左子树DFS就更新它，否则不更新。因为如果往左子树找，中序遍历的下一个节点就是lastVisited；
如果找不到p，返回NULL；
如果找到了p，先判断它是否有右子树，如果有，就返回右子树的最小值(依然用DFS求, O(h))；否则返回lastVisited。

class Solution {
public:
    TreeNode *lastVisited;
    TreeNode* inorderSuccessor(TreeNode* root, TreeNode* p) {
        /*  idea:
            1. find p, O(h)
            2. if p->right is not NULL, calculate the minimum value in the right subtree of p, O(h)
               else return the last visited node(inorder parent)
        */
        if (root == NULL) {
            return NULL;
        }

        if (findTarget(root, p)) {
            if (p->right != NULL) {
                return dfsMin(p->right);
            } else {
                return lastVisited;
            }
        } else {
            return NULL;
        }
    }

private:
    bool findTarget(TreeNode* root, TreeNode* p) {
        if (root == NULL) {
            return false;
        }

        lastVisited = NULL;
        while (root != NULL) {
            if (root == p) {
                return true;
            }
            if (root->val < p->val) {
                root = root->right;
            } else {
                lastVisited = root;
                root = root->left;
            }
        }
        return false;
    }

    TreeNode* dfsMin(TreeNode* root) {
        if (root == NULL) {
            return NULL;
        }
        while (root->left != NULL) {
            root = root->left;
        }
        return root;
    }
};

LintCode 86: Binary Search Tree Iterator (二叉查找树迭代器)

/**
 * Definition of TreeNode:
 * class TreeNode {
 * public:
 *     int val;
 *     TreeNode *left, *right;
 *     TreeNode(int val) {
 *         this->val = val;
 *         this->left = this->right = NULL;
 *     }
 * }
 * Example of iterate a tree:
 * BSTIterator iterator = BSTIterator(root);
 * while (iterator.hasNext()) {
 *    TreeNode * node = iterator.next();
 *    do something for node
 */
class BSTIterator {
public:
    stack<TreeNode *> mystack;
    TreeNode *current;
    //@param root: The root of binary tree.
    BSTIterator(TreeNode *root) {
        while (!mystack.empty()) {
            mystack.pop();
        }
        current = root;
    }

    //@return: True if there has next node, or false
    bool hasNext() {
        return (current != NULL || !mystack.empty());
    }
    
    //@return: return next node
    TreeNode* next() {
        while (current != NULL) {
            mystack.push(current);
            current = current->left;
        }
        current = mystack.top();
        mystack.pop();
        TreeNode *rtn = current;
        current = current->right;
        return rtn;
    }
};

注意点:

构造函数的初始化：清栈
next()函数用中序遍历写

LintCode 11: Search Range in Binary Search Tree (二叉查找树中搜索区间)

思路：中序遍历加一个判断即可。中序遍历的非递归写法要烂熟于心！

class Solution {
public:
    /**
     * @param root: The root of the binary search tree.
     * @param k1 and k2: range k1 to k2.
     * @return: Return all keys that k1<=key<=k2 in ascending order.
     */
    vector<int> searchRange(TreeNode* root, int k1, int k2) {
        vector<int> rst;
        if (root == NULL) {
            return rst;
        }

        stack<TreeNode*> mystack;
        TreeNode *current = root;
        while (current != NULL || !mystack.empty()) {
            while (current != NULL) {
                mystack.push(current);
                current = current->left;
            }
            current = mystack.top(); mystack.pop();
            if (current->val >= k1 && current->val <= k2) {
                rst.push_back(current->val);
            }
            if (current->val > k2) {
                return rst;
            }
            current = current->right;
        }

        return rst;
    }
};

LintCode 85: Insert Node in a Binary Search Tree (在二叉查找树中插入节点)

思路1：中序遍历（不推荐）

中序遍历，用一个变量lastVisited记录上一次访问的节点(初始化为null)
如果能找到第一个大于node的节点。如果这个节点是根节点，则将node插入其左边，返回；否则判断lastVisited是不是叶子节点，是的话就插入其右边，不是就插入当前节点的左边，返回；
如果找不到一个大于node的节点，则将node插入lastVisited的右边，返回。

class Solution {
public:
    /**
     * @param root: The root of the binary search tree.
     * @param node: insert this node into the binary search tree
     * @return: The root of the new binary search tree.
     */
    TreeNode* insertNode(TreeNode* root, TreeNode* node) {
        if (root == NULL) {
            return node;
        }
        // inorder traversal, to find the first node with a larger value
        stack<TreeNode*> mystack;
        TreeNode *current = root, *lastVisited = NULL;
        while (current != NULL || !mystack.empty()) {
            while (current != NULL) {
                mystack.push(current);
                current = current->left;
            }
            current = mystack.top(); mystack.pop();
            if (current->val > node->val) {
                if (lastVisited == NULL) {
                    current->left = node;
                    return root;    // 因为这句没加，debug了好久==
                }
                if (lastVisited->right == NULL) {
                    lastVisited->right = node;
                } else {
                    current->left = node;
                }
                return root;
            }
            lastVisited = current;
            current = current->right;
        }
        // if not find
        if (lastVisited != NULL) {
            lastVisited->right = node;
        }

        return root;
    }
};

思路2：递归，代码很简洁。

class Solution {
public:
    /**
     * @param root: The root of the binary search tree.
     * @param node: insert this node into the binary search tree
     * @return: The root of the new binary search tree.
     */
    TreeNode* insertNode(TreeNode* root, TreeNode* node) {
        if (root == NULL) {
            root = node;
            return root;
        }
        if (root->val < node->val) {
            root->right = insertNode(root->right, node);
        }
        if (root->val > node->val) {
            root->left = insertNode(root->left, node);
        }
        return root;
    }
};

思路3：非递归，首先要明确一个事实：节点一定是被插在二叉搜索树的叶子节点后的，知道了这个事实，就好办了。DFS时每次将当前节点的值与node的值作比较，如果比node小就往右走，否则往左走，直到叶子节点。为了方便最后的插入操作，需要用一个变量记录上一次访问的节点。

class Solution {
public:
    /**
     * @param root: The root of the binary search tree.
     * @param node: insert this node into the binary search tree
     * @return: The root of the new binary search tree.
     */
    TreeNode* insertNode(TreeNode* root, TreeNode* node) {
        if (root == NULL) {
            root = node;
            return root;
        }
        TreeNode *curt = root, *lastVis = NULL;
        while (curt != NULL) {
            lastVis = curt;
            if (curt->val < node->val) {
                curt = curt->right;
            } else {
                curt = curt->left;
            }
        }
        if (lastVis->val < node->val) {
            lastVis->right = node;
        } else {
            lastVis->left = node;
        }
        return root;
    }
};

LintCode 87: Remove Node in Binary Search Tree (删除二叉查找树的节点)

这题思路并不难想，但是实现起来不容易。

思路：

找到目标节点和它的父节点。用递归做，复杂度O(h)，h是BST的高。这里有个小技巧，用一个dummy node指向根节点，比如dummy->left = root，最后返回dummy->left就行了，这是因为被删除的目标节点可能就是根节点。
删除目标节点。这一步比较难。《算法导论》上有关于该问题的讨论，常用的思路是分三种情况讨论：目标节点没有孩子、目标节点有一个孩子，以及目标节点有两个孩子。第一种情况最好处理，只要将目标节点设为空就好了，target = NULL；第二种情况就将目标节点父节点指向目标节点的孩子；第三种情况最复杂，下面详细讨论。虽然这个思路很清晰，但是实现起来你会发现代码比较长，不简洁。其实只要分目标节点有无右子树两种情况来讨论就能处理了，详细分析如下： 2.1 目标节点无右子树。只要将目标节点的父节点指向目标节点的左子树就好。（少了很多判断，比上面的第二种情况简洁多了）但是如果目标节点也没有左子树怎么办呀？这就变成上面的第一种情况了，目标节点的父节点指向的是一个空指针，依然可以； 2.2 目标节点有右子树。（即上面的第三种情况的处理方法，请结合下面的图解）首先DFS找到目标节点右子树的最小值，它在右子树的最左下角；然后删掉这个点，注意这个点不可能有左子树（否则它一定不是最小的），但是可能有右子树，所以直接将这个点的父节点指向该点的右子树就好，这里要用到父节点，前一步DFS时用一个变量保存即可；最后将目标节点的值修改为前一步被删掉节点的值。注意这里并没有删掉目标节点，而是替换值。因为将值替换为了它右子树的最小值，而第二步就将有最小值的节点删掉了，所以保证了新得到的树依然是BST。

不难得到复杂度是O(h)

2.2的图解： remove-bst-1 目标节点值为12

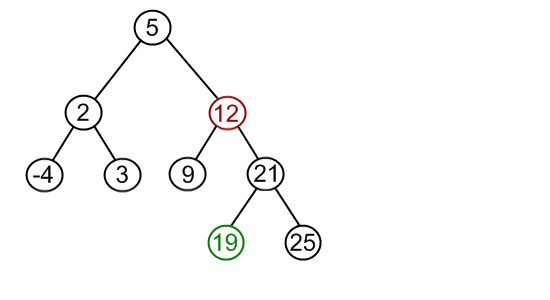remove-bst-2 找到目标节点右子树的最小值

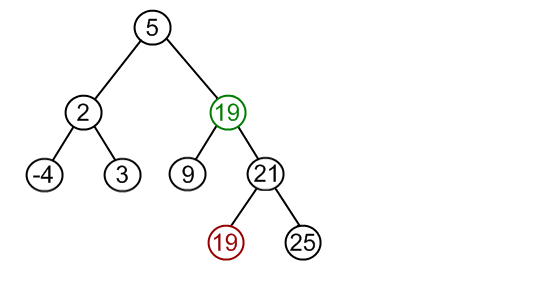remove-bst-3 替换目标节点的值

remove-bst-4 删除目标节点右子树的最小节点

图片来源: <a href=”http://www.algolist.net/Data_structures/Binary_search_tree/Removal”, target=”_blank”>http://www.algolist.net/Data_structures/Binary_search_tree/Removal </a>

class Solution {
public:
    /**
     * @param root: The root of the binary search tree.
     * @param value: Remove the node with given value.
     * @return: The root of the binary search tree after removal.
     */
    TreeNode* removeNode(TreeNode* root, int value) {
        if (root == NULL) {
            return root;
        }
        
        TreeNode *dummy = new TreeNode(0);
        dummy->left = root;
        
        TreeNode *targetParent = findNode(root, value, dummy);
        TreeNode *target;
        if (targetParent->left != NULL && targetParent->left->val == value) {
            target = targetParent->left;
        } else if (targetParent->right != NULL && targetParent->right->val == value) {
            target = targetParent->right;
        } else {
            return dummy->left;
        }
        
        deleteNode(targetParent, target);
        
        return dummy->left;    // 为什么不是return root? 因为root可能会被删掉
    }

private:
    TreeNode* findNode(TreeNode* root, int value, TreeNode* parent) {
        // if find the node, return its parent
        if (root == NULL) {
            return parent;
        }
        if (root->val == value) {
            return parent;
        }
        if (root->val < value) {
            return findNode(root->right, value, root);
        } else {
            return findNode(root->left, value, root);
        }
    }
    
    void deleteNode(TreeNode* targetParent, TreeNode* target) {
        if (target->right == NULL) {
            if (targetParent->left == target) {
                targetParent->left = target->left;
            } else {
                targetParent->right = target->left;
            }
        } else {
            TreeNode *curt = target->right;
            TreeNode *father = target;
            while (curt->left != NULL) {
                father = curt;
                curt = curt->left;
            }
            if (father->left == curt) {
                father->left = curt->right;
            } else {
                father->right = curt->right;
            }
            target->val = curt->val;
        }
    }
};

参考了这里，总感觉九章算法的代码写得清晰又简洁~

Lintcode 376: Binary Tree Path Sum (二叉树的路径和)

首先要理解题意。只考虑根节点到叶子节点的路径，分治法就能做。深深感觉到分治的强大~

class Solution {
public:
    /**
     * @param root the root of binary tree
     * @param target an integer
     * @return all valid paths
     */
    vector<vector<int>> binaryTreePathSum(TreeNode *root, int target) {
        vector<vector<int> > rst;
        if (root == NULL) {    // 当root->val > target时，也可以加入，因为节点可能为负！
            return rst;
        }
        if (root->val == target) {
            vector<int> tmp(1,root->val);
            rst.push_back(tmp);
            return rst;
        }
        // divide
        vector<vector<int> > left = binaryTreePathSum(root->left, target - root->val);
        vector<vector<int> > right = binaryTreePathSum(root->right, target - root->val);
        // conquer (把root->val插入子树结果中每条路径的首部)
        for (int i = 0; i < left.size(); ++i) {
            left[i].insert(left[i].begin(), root->val);
        }
        for (int i = 0; i < right.size(); ++i) {
            right[i].insert(right[i].begin(), root->val);
        }
        left.insert(left.end(), right.begin(), right.end());
        
        return left;
    }
};

LintCode 469: Identical Binary Tree (等价二叉树)

思路：分治。

class Solution {
public:
    /**
     * @aaram a, b, the root of binary trees.
     * @return true if they are identical, or false.
     */
    bool isIdentical(TreeNode* a, TreeNode* b) {
        if (a == NULL && b == NULL) {
            return true;
        }
        if (a == NULL || b == NULL) {
            return false;
        }
        if (a->val != b->val) {
            return false;
        }
        bool cas1 = isIdentical(a->left, b->left);
        if (!cas1) { return false; }
        bool cas2 = isIdentical(a->right, b->right);
        if (!cas2) { return false; }
        return true;
    }
};

LintCode 468: Symmetric Binary Tree (对称二叉树)

思路1：把根节点的右子树（或者左子树）反转，然后判断左、右子树是否等价。

class Solution {
public:
    /**
     * @param root, the root of binary tree.
     * @return true if it is a mirror of itself, or false.
     */
    bool isSymmetric(TreeNode* root) {
        if (root == NULL) {
            return true;
        }
        reverseTree(root->right);
        if (isIdentical(root->left, root->right)) {
            return true;
        } else {
            return false;
        }
    }
private:
    void reverseTree(TreeNode *root) {
        if (root == NULL) {
            return;
        }
        // swap left subtree and right subtree
        TreeNode *tmp = new TreeNode(0);
        tmp->left = root->right; tmp->right = root->left;
        root->left = tmp->left;
        root->right = tmp->right;
        
        reverseTree(root->left);
        reverseTree(root->right);
    }

    bool isIdentical(TreeNode* a, TreeNode* b) {
        if (a == NULL && b == NULL) {
            return true;
        }
        if (a == NULL || b == NULL) {
            return false;
        }
        if (a->val != b->val) {
            return false;
        }
        bool cas1 = isIdentical(a->left, b->left);
        if (!cas1) { return false; }
        bool cas2 = isIdentical(a->right, b->right);
        if (!cas2) { return false; }
        return true;
    }    
};

思路2：将判断等价二叉树的方法稍作修改。

class Solution {
public:
    /**
     * @param root, the root of binary tree.
     * @return true if it is a mirror of itself, or false.
     */
    bool isSymmetric(TreeNode* root) {
        if (root == NULL) {
            return true;
        }
        return check(root->left, root->right);
    }
private:
    bool check(TreeNode* root1, TreeNode* root2) {
        if (root1 == NULL && root2 == NULL) {
            return true;
        }
        if (root1 == NULL || root2 == NULL) {
            return false;
        }
        if (root1->val != root2->val) {
            return false;
        }
        return check(root1->left, root2->right) && check(root1->right, root2->left);
    }
};

LintCode 467: Complete Binary Tree (完全二叉树)

判断一棵二叉树是否是完全二叉树。完全二叉树，就是节点按层从左到右添加，只有一个节点有了左孩子，才能添加右孩子；只有上一层填满，才能填下一层。满二叉树则是除了叶子节点，所有的节点都有左孩子和右孩子。

思路：

首先判断左、右子树是不是完全二叉树，有一个不是的话，就返回false；
如果左、右子树都是完全二叉树，则还要比较它们的高度。如果左子树的高度小于右子树，返回false；如果左子树的高度等于右子树，再判断左子树是不是满二叉树，如果不是，返回false；如果左子树高度比右子树高度大2（或以上），返回false；如果左子树高度恰好比右子树高度大1，再判断右子树是不是满二叉树，如果不是，返回false；若都通过了上面的检测，返回true。

class Solution {
public:
    /**
     * @param root, the root of binary tree.
     * @return true if it is a complete binary tree, or false.
     */
    bool isComplete(TreeNode* root) {
        if (root == NULL) {
            return true;
        }
        bool left = isComplete(root->left);
        if (!left) { return false; }
        bool right = isComplete(root->right);
        if (!right) { return false; }
        int lefth = maxDepth(root->left);
        int righth = maxDepth(root->right);
        if (lefth < righth) {
            return false;
        }
        if (lefth == righth && !isFull(root->left)) {
            return false;
        }
        if (lefth - righth > 1) {
            return false;
        }
        if (lefth - righth == 1 && !isFull(root->right)) {
            return false;
        }

        return true;
    }
    
    int maxDepth(TreeNode* root) {
        if (root == NULL) {
            return 0;
        }
        int left = maxDepth(root->left);
        int right = maxDepth(root->right);
        return 1 + max(left, right);
    }
    
    bool isFull(TreeNode *root) {
        if (root == NULL) {
            return true;
        }
        if (root->left == NULL && root->right == NULL) {
            return true;
        }
        if (root->left == NULL || root->right == NULL) {
            return false;
        }
        if (!isFull(root->left)) {
            return false;
        }
        if (!isFull(root->right)) {
            return false;
        }
        return true;
    }
};

LintCode 155: Minimum Depth of Binary Tree (二叉树的最小深度)

首先要弄清“最小深度”以及“叶子节点”的概念。这题不难，但是容易错。

class Solution {
public:
    /**
     * @param root: The root of binary tree.
     * @return: An integer
     */
    int minDepth(TreeNode *root) {
        if (root == NULL) {
            return 0;
        }
        if (root->left == NULL) {
            return 1 + minDepth(root->right);
        }
        if (root->right == NULL) {
            return 1 + minDepth(root->left);
        }
        return 1 + min(minDepth(root->left), minDepth(root->right));
    }
};

LintCode 73: Construct Binary Tree from Preorder and Inorder Traversal (前序遍历和中序遍历构造二叉树)

很好的题。递归，分别构造左子树和右子树，然后合并。通过前序遍历和中序遍历的结果可以计算出左子树的节点个数，据此可以知道左子树的前序遍历和中序遍历；右子树同理。

写递归函数时，边界要细心处理。

class Solution {
    /**
     *@param preorder : A list of integers that preorder traversal of a tree
     *@param inorder : A list of integers that inorder traversal of a tree
     *@return : Root of a tree
     */
public:
    TreeNode *buildTree(vector<int> &preorder, vector<int> &inorder) {
        if (preorder.empty()) {
            return NULL;
        }
        return helper(preorder, inorder, 0, preorder.size() - 1, 0, inorder.size() - 1);
    }

private:
    TreeNode *helper(vector<int>& preorder, vector<int>& inorder, int ps, int pe, int is, int ie) {
        if (ps > pe) {
            return NULL;
        }
        TreeNode* root = new TreeNode(preorder[ps]);
        int pos;
        for (int i = is; i <= ie; ++i) {
            if (inorder[i] == root->val) {
                pos = i;
                break;
            }
        }
        root->left = helper(preorder, inorder, ps + 1, ps + pos - is, is, pos - 1);
        root->right = helper(preorder, inorder, ps + pos - is + 1, pe, pos + 1, ie);
        return root;
    }
};

LintCode 72: Construct Binary Tree from Inorder and Postorder Traversal (中序遍历和后序遍历构造二叉树)

与前面思路一样。

class Solution {
    /**
     *@param inorder : A list of integers that inorder traversal of a tree
     *@param postorder : A list of integers that postorder traversal of a tree
     *@return : Root of a tree
     */
public:
    TreeNode *buildTree(vector<int> &inorder, vector<int> &postorder) {
        if (inorder.empty()) {
            return NULL;
        }
        return helper(inorder, postorder, 0, inorder.size() - 1, 0, postorder.size() - 1);
    }
    
private:
    TreeNode *helper(vector<int> &inorder, vector<int> &postorder, int instart, int inend, int poststart, int postend) {
        if (instart > inend) {
            return NULL;
        }
        TreeNode* root = new TreeNode(postorder[postend]);
        int pos;
        for (int i = instart; i <= inend; ++i) {
            if (inorder[i] == root->val) {
                pos = i;
                break;
            }
        }
        root->left = helper(inorder, postorder, instart, pos - 1, poststart, poststart + pos - instart - 1);
        root->right = helper(inorder, postorder, pos + 1, inend, poststart + pos - instart, postend - 1);
        return root;
    }
};

LintCode 7: Binary Tree Serialization (二叉树的序列化和解序列)

这题调试了好久。主要是对string的操作很不熟悉，代码也写得不简洁。

思路（基于层序遍历，即BFS）：

序列化：层序遍历即可，不同的是当节点的孩子为空时，要把它解释成特殊符号（比如#）再放入string；这里不一定要用队列，vector容器就可以。另外，用std::to_string将整数转为string类型。
解序列：一边BFS，一边建二叉树。我用了两个整型变量posStart和posEnd来记录真正有意义的子序列（即字符,之间的部分）的左、右边界，用STL中的string::substr函数提取这两个边界之间的子串，用std::stoi将string类型转为int型。

注意：std::to_string和std::stoi都是C++11版本及以上提供的库函数。

class Solution {
public:
    /**
     * This method will be invoked first, you should design your own algorithm
     * to serialize a binary tree which denote by a root node to a string which
     * can be easily deserialized by your own "deserialize" method later.
     */
    string serialize(TreeNode *root) {
        string binaryTree;
        if (root == NULL) {
            return binaryTree;
        }
        
        vector<TreeNode*> myqueue;
        myqueue.push_back(root);
        
        for (int i = 0; i < myqueue.size(); ++i) {
            TreeNode *node = myqueue[i];
            if (node == NULL) {
                continue;
            }
            myqueue.push_back(node->left);
            myqueue.push_back(node->right);
        }
        
        //while (myqueue[myqueue.size() - 1] == NULL) {
        //    myqueue.pop_back();
        //}
        
        for (int i = 0; i < myqueue.size(); ++i) {
            if (myqueue[i] == NULL) {
                binaryTree = binaryTree + "#,";
            } else {
                binaryTree = binaryTree + to_string(myqueue[i]->val);
                binaryTree = binaryTree + ",";
            }
        }

        return binaryTree;
    }

    /**
     * This method will be invoked second, the argument data is what exactly
     * you serialized at method "serialize", that means the data is not given by
     * system, it's given by your own serialize method. So the format of data is
     * designed by yourself, and deserialize it here as you serialize it in
     * "serialize" method.
     */
    TreeNode *deserialize(string data) {
        if (data.empty()) {
            return NULL;
        }
        
        int posStart = 0, posEnd = data.find(",", posStart);
        //cout << stoi(data.substr(posStart, posEnd - posStart)) << " ";
        TreeNode *root = new TreeNode(stoi(data.substr(posStart, posEnd - posStart)));
        posStart = posEnd + 1;
        
        queue<TreeNode*> myqueue;
        myqueue.push(root);
        TreeNode *curt;
        while (!myqueue.empty() && posStart < data.size()) {
            curt = myqueue.front();
            posEnd = data.find(",", posStart);
            string node = data.substr(posStart, posEnd - posStart);
            // left subtree
            if (node[0] != '#') {
                TreeNode *left = new TreeNode(stoi(node));
                curt->left = left;
                myqueue.push(left);
                posStart = posEnd + 1;
            }
            posStart = posEnd + 1;
            posEnd = data.find(",", posStart);
            // right subtree
            node = data.substr(posStart, posEnd - posStart);
            if (node[0] != '#') {
                TreeNode *right = new TreeNode(stoi(node));
                curt->right = right;
                myqueue.push(right);
                posStart = posEnd + 1;
            }
            posStart = posEnd + 1;
            posEnd = data.find(",", posStart);
            myqueue.pop();
        }
        
        return root;
    }
};

-----EOF-----

Categories: 算法 Tags: 二叉树